Movimiento Parabólico
TIRO SEMIPARABOLICO (lanzamiento Horizontal)

Las magnitudes involucradas son:
- Velocidad inicial (Vi)
- Altura de la mesa (H)
- Alcance (R)
- Tiempo de vuelo (tv)
Para responder estas preguntas debemos hacer un análisis del movimiento.
El movimiento del objeto se puede descomponer en dos, uno horizontal y otro vertical.
- Horizontal: es un movimiento rectilineo uniforme con una velocidad que es la misma velocidad que llevaba la esfera cuando empieza su caida.
- Vertical: es un movimiento unifórmemente acelerado correspondiente a una "caida libre" desde la altura H.
El tiempo que se tarda en caer es el mismo que se tarda en avanzar En otras palabras, el tiempo que tarda el objeto para recorrer x es el mismo tiempo que tarda para llegar a y.
Alcance y tiempo de vuelo.
Nos dá la distancia d que "cae" un objeto que se suelta desde una altura transcurrido un tiempo t.
Nos dá la distancia que "avanza" un objeto que se desplaza con movimiento uniforme transcurrido un tiempo t.
Despejando t en ambas ecuaciones.
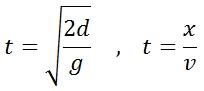
Igualando:

Obsérvese que cuando la distancia que se ha caido es H (d=H) , la distancia que se ha avanzado es R (x=R), entonces:

Ecuación nos dá el "alcance" R en función de la velocidad inicial y la altura desde donde cae lel objeto.
Para hallar el "tiempo de vuelo" (tv) o sea el tiempo que tarda el objeto entre el momento en que se lanza y el momento en que impacta el suelo acudimos a la componente horizontal del movimiento (movimiento rectilineo uniforme).
El tiempo, conocida la velocidad, viene dado por t=d/v (distancia recorrida sobre velocidad). Si la distancia recorrida es R (el alcance) entonecs el tiempo de vuelo tv está dado por:

Le colocamos a v el subindice x (vx) para indicar que se trata de la velocidad en el sentido del eje X.
Ecuación de la trayectoria semiparabólica.
Encontraremos la ecuación matemática que nos dé la ordenada y en función de la abcisa x para así poder determinar exáctamente por donde pasa el objeto. Esto puede ser útil si queremos saber si habrá impacto, o nó, con otro objeto.
Anteriormente habíamos llegado a la expresión:

Si analizamos la figura que encabeza esta página vemos que se cumple d=H-y. Entonces si reemplazamos d obtenemos:

que corresponde a la ecuación de una parábola de la forma:
De ahí el nombre de movimiento parabólico.
ECUACIÓN DEL TIRO PARABÓLICO
Ecuaciones con ejes trasladados
Si conocemos la ecuación de una gráfica en sistema XY, podemos encontrar la ecuación de la misma gráfica en un nuevo sistema trasladado respecto al original.
Sea XY el sistema respecto al cual una gráfica tiene la ecuación y=f(x), entonces respecto a un sistema X'Y' trasladado cuyo origen sea el punto (h,k), la misma gráfica tendrá una ecuación y+h=f(x+k)
Si, por ejemplo, queremos Determinar la nueva ecuación de la recta 2x+4y-6=0 después de trasladar los ejes a un nuevo origen cuyas coordenadas son (2,4).
Lo que debemos hacer es:
h=2, k=4 ➫ x=x'+2, y=y'+4
2x+4y-6=0 ➫ 2(x'+2)+4(y'+4)-6
2x'+4+4y'+16-6=0=2x'+4y'+14=0
Podemos escribir x en lugar de x' y y en lugar de y' para obtener la nueva ecuación:
2x+4y+14=0
read more

Pero ahora respecto a un nuevo sistema de coordenadas X'Y' cuyo orígen es el punto

respecto a XY. Entonces la nueva ecuación sería:

Esta ecuación nos dá el valor de y para un valor dado de x, es decir nos dá los puntos por donde pasa el objeto arrojado en función de v (componente horizontal de la velocidad con que se arroja) y de la altura máxima que alcanza (H). Estos parámetros no son controlables por el lanzador quien sólo puede medir la velocidad inicial con que arroja el objeto y el ángulo alfa que ésta forma con la horizontal.
Trabajamos algebraicamente la ecuación:

Esta es la ecuación de la trayectoria que sigue un objeto que se lanza con una velocidad vo en una dirección que forma un ángulo alfa con la horizontal.
En el siguiente enlace se entra a una aplicación Desmos en la que se pueden variar los parámetros vo y alfa y observar el comportamiento de la trayectoria parabola: